いつもお世話になっております。
すみません、また教えていただきたいのですが、
下記の円のxの角度を出す際に円周角の定理をどう利用すればよろしいでしょうか?問題集には下記の公式しか乗っていないので分かりにくいので教えていただけますと幸いです。
下記の円のxの角度を出す際に円周角の定理をどう利用すればよろしいでしょうか?問題集には下記の公式しか乗っていないので分かりにくいので教えていただけますと幸いです。
Re: いつも
ブーメランの公式
以下リンク参照。
https://mathtext.info/blog/2020/05/17/chu2bume20200517/
以下リンク参照。
https://mathtext.info/blog/2020/05/17/chu2bume20200517/
いつもお世話になっております。
 通りすがり
通りすがり  2022/09/09(Fri) 19:59 No.20
2022/09/09(Fri) 19:59 No.20
ありがとうございます!毎回分かり易い解き方に加えてURLもアップしていただきお手数をおかけしました。
 通りすがり
通りすがり  2022/09/09(Fri) 19:59 No.20
2022/09/09(Fri) 19:59 No.20
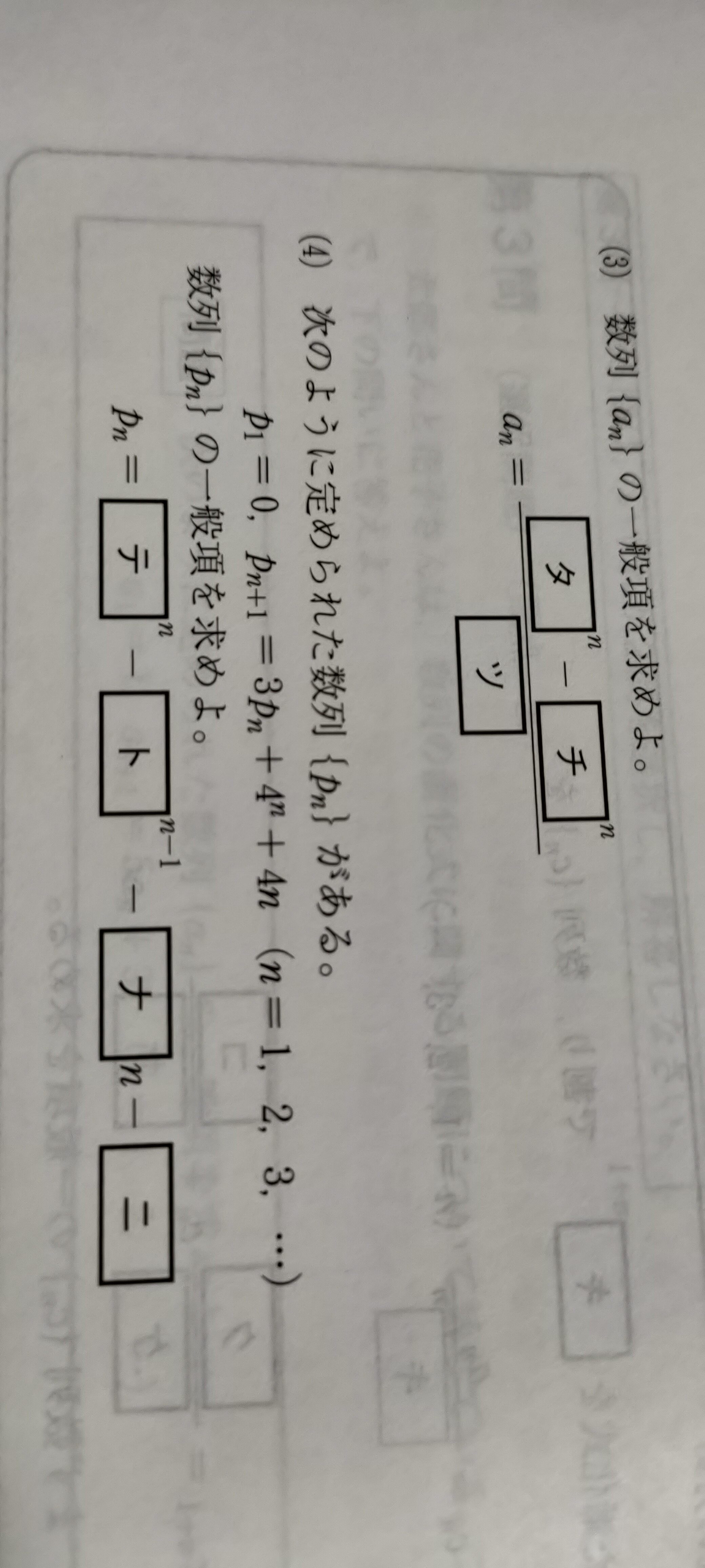
数列の問題
Re: 数列の問題
 CORNO
CORNO  2022/09/03(Sat) 06:50 No.10
2022/09/03(Sat) 06:50 No.10
おはようございます.CORNOです.
なかなかたいへんな問題ですね.
解説には時間がかかるかもしれません.急ぐのであれば,私には無理ですので退出します.
回答の前に,前沢さんに確認したいことがあります.
学年を教えてください.
それと,次の漸化式は2つとも解けますか?
回答を書き込まなくていいです.「解ける」or「解けない」だけ書き込んでください.
(1) x[1]=1,x[n+1]=2x[n]-3
(2) x[1]=1,x[n+1]=2x[n]+3^n ←^n はn乗を表します
なかなかたいへんな問題ですね.
解説には時間がかかるかもしれません.急ぐのであれば,私には無理ですので退出します.
回答の前に,前沢さんに確認したいことがあります.
学年を教えてください.
それと,次の漸化式は2つとも解けますか?
回答を書き込まなくていいです.「解ける」or「解けない」だけ書き込んでください.
(1) x[1]=1,x[n+1]=2x[n]-3
(2) x[1]=1,x[n+1]=2x[n]+3^n ←^n はn乗を表します
 CORNO
CORNO  2022/09/03(Sat) 06:50 No.10
2022/09/03(Sat) 06:50 No.10
Re: 数列の問題
こんにちは。ご返信、ありがとうございます。
学年は高3年で、2つの漸化式は解けます。
よろしくお願いします。
学年は高3年で、2つの漸化式は解けます。
よろしくお願いします。
Re: 数列の問題
 CORNO
CORNO  2022/09/03(Sat) 17:18 No.15
2022/09/03(Sat) 17:18 No.15
管理人さんの解説で解決したのではないですか.
 CORNO
CORNO  2022/09/03(Sat) 17:18 No.15
2022/09/03(Sat) 17:18 No.15
Re: 数列の問題
すみません。
仮定式の置き方で定数がつく点が少し不安で、
他のアドバイスが頂けるかと質問を続けてしまいました。
ほぼ解決しましたので、これにて完了とさせていただきます。
ご協力大変ありがとうございました。
仮定式の置き方で定数がつく点が少し不安で、
他のアドバイスが頂けるかと質問を続けてしまいました。
ほぼ解決しましたので、これにて完了とさせていただきます。
ご協力大変ありがとうございました。
数列の問題
Re: 数列の問題
おはようございます。
多分漸化式を解くってことは
等差系, 等比系, 階差系なんかに落ち着かなきゃ解けないってことですよね。多分。それで漸化式見ると
p_(n+1)=3p_n+4ⁿ+4n・・・①ってなってますよね。この3P_nの3がなければ階差系で解けるはずなんですが,
3があるので等比系にもっていかないと漸化式が解けないんですよ。きっと。
ですからq_n=p_n+x4ⁿ+yn+z・・・②っておいてるんだと思います。
このときこの漸化式は
q_(n+1)=3q_nに帰着しないと漸化式自体が解けません。
そういったことから②のようにおいて漸化式を解くのだと思います。
そして
p_(n+1)+x4ⁿ⁺¹+y(n+1)+z=3(p_n+x4ⁿ+yn+z)
p_(n+1)=3p_n-x4ⁿ+2yn-y+2z・・・③
となり, ①と③が恒等的な関係より
-x=1
2y=4
-y+2z=0
から, x=-1, y=2, z=1を出して
漸化式を書くと
p_(n+1)-4ⁿ⁺¹+2(n+1)+1=3(p_n-4ⁿ+2n+1)
となり、これは初項
p_1-4+2+1=0-1=-1, 公比3の等比数列なので,
p_n-4ⁿ+2n+1=-3ⁿ⁻¹
よって,
p_n=4ⁿ-3ⁿ⁻¹-2n-1
_(n+1)は下付き文字を表します。
じゃないかな?と思う次第です。
では。
お互い数学得意になりましょう。
多分漸化式を解くってことは
等差系, 等比系, 階差系なんかに落ち着かなきゃ解けないってことですよね。多分。それで漸化式見ると
p_(n+1)=3p_n+4ⁿ+4n・・・①ってなってますよね。この3P_nの3がなければ階差系で解けるはずなんですが,
3があるので等比系にもっていかないと漸化式が解けないんですよ。きっと。
ですからq_n=p_n+x4ⁿ+yn+z・・・②っておいてるんだと思います。
このときこの漸化式は
q_(n+1)=3q_nに帰着しないと漸化式自体が解けません。
そういったことから②のようにおいて漸化式を解くのだと思います。
そして
p_(n+1)+x4ⁿ⁺¹+y(n+1)+z=3(p_n+x4ⁿ+yn+z)
p_(n+1)=3p_n-x4ⁿ+2yn-y+2z・・・③
となり, ①と③が恒等的な関係より
-x=1
2y=4
-y+2z=0
から, x=-1, y=2, z=1を出して
漸化式を書くと
p_(n+1)-4ⁿ⁺¹+2(n+1)+1=3(p_n-4ⁿ+2n+1)
となり、これは初項
p_1-4+2+1=0-1=-1, 公比3の等比数列なので,
p_n-4ⁿ+2n+1=-3ⁿ⁻¹
よって,
p_n=4ⁿ-3ⁿ⁻¹-2n-1
_(n+1)は下付き文字を表します。
じゃないかな?と思う次第です。
では。
お互い数学得意になりましょう。
Re: 数列の問題
ありがとうございました
仮定式を置くときに
q_n=p_n+x4ⁿ+yn と定数なしでおいてしまいそうです...
気をつけていきます。
詳しい解説をありがとうございました。
仮定式を置くときに
q_n=p_n+x4ⁿ+yn と定数なしでおいてしまいそうです...
気をつけていきます。
詳しい解説をありがとうございました。
掲示板リニューアル
質問掲示板新しくしました。
小さな2乗の文字とかが使えるようになりました。
スマホ対応になりました。
小さな2乗の文字とかが使えるようになりました。
スマホ対応になりました。
√45n
√45nが自然数になるための最小の自然数nを求めよ。
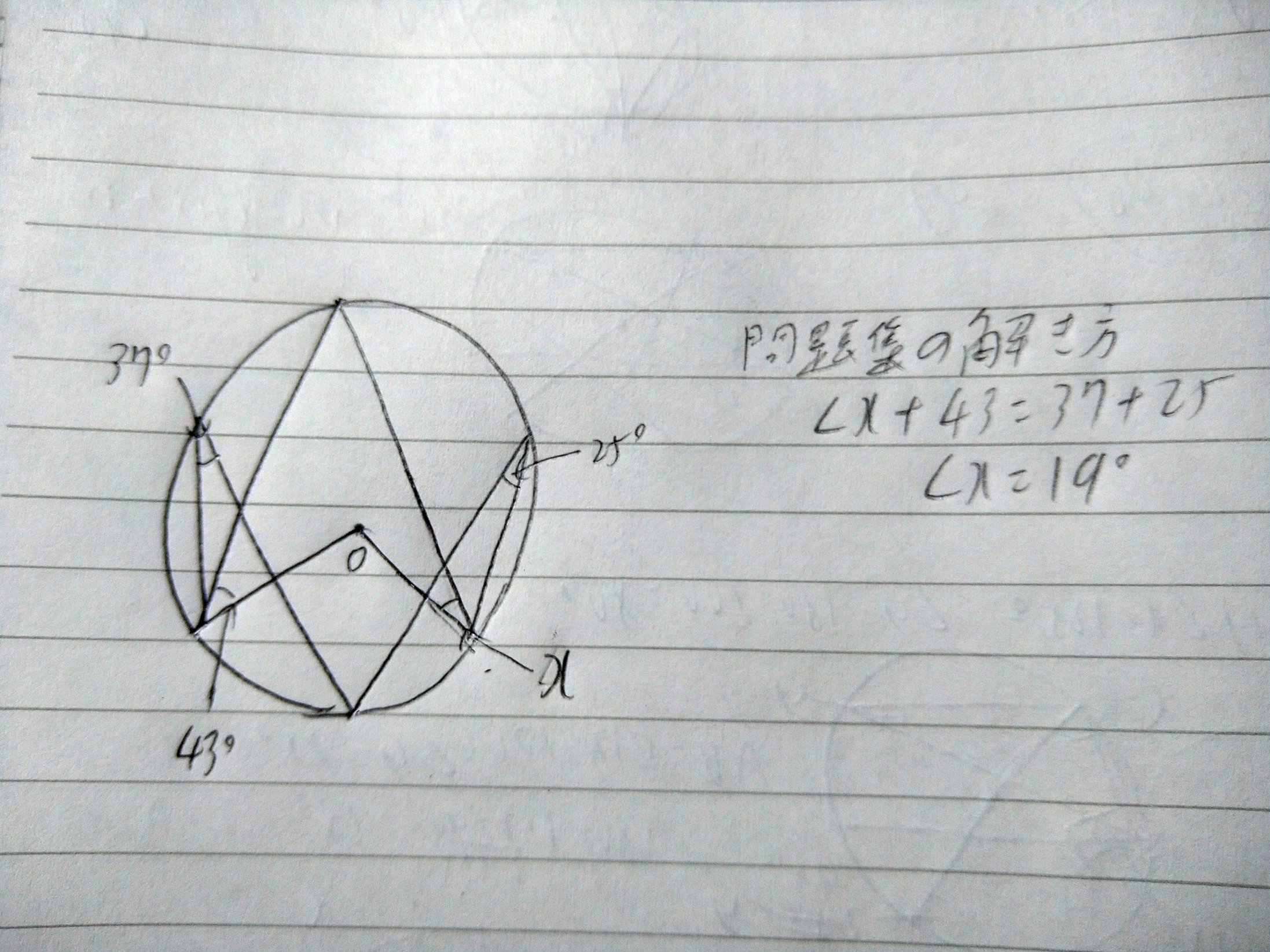
 通りすがり
通りすがり