最大と最小
こんにちは
何卒宜しくお願い致します。
何卒宜しくお願い致します。
Re: 最大と最小
管理人 
2023/02/10(Fri) 01:07 No.55
こんばんは。
あっしの手には負えないので、
知恵袋からの引用と少し付けたし
00年東大文系
f(x，y)=1-ax-by-axy
fをxの関数と見れば高々1次式(一次関数)．
よって，最小になりうるのはx=-1 or 1のとき．
fをyの関数と見れば，高々1次式(一次関数)．
よって，最小になりうるのはx=-1 or 1のとき．
よって，-1≦x≦1，-1≦y≦1 におけるf(x，y)の
最小値の候補は
f(-1,-1)，f(-1，1)，f(1，-1)，f(1，1)しかなく，
これらがすべて正であることが必要十分．
f(-1,-1)=b+1>0
f(-1，1)=1+2a-b>0
f(1，-1)=1+b>0
f(1，1)=1-2a-b>0
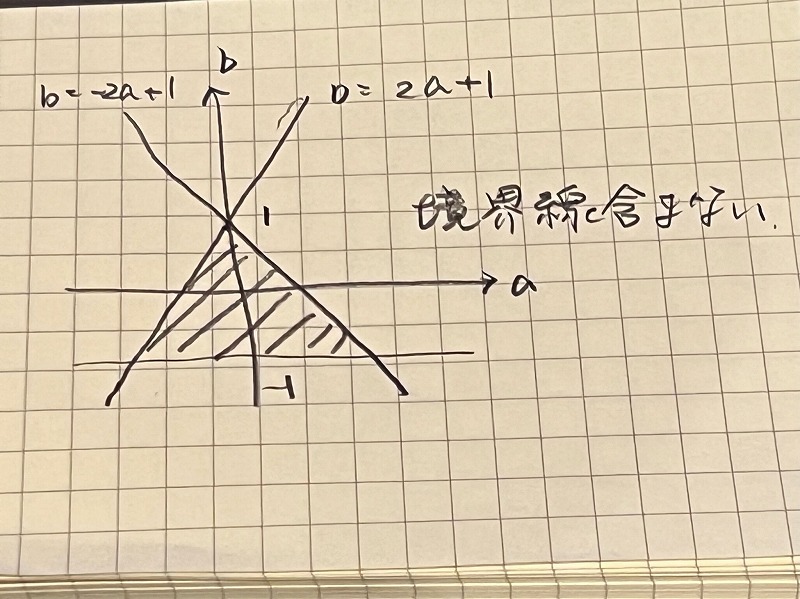
以上より，-1<b かつ b<-2a+1 かつ b<2a+1
リンク
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1452773619?fr=sc_scdd&__ysp=eHnlubPpnaLjga7poJjln58gLTHiiaZ4IDEtYXgtYnktYXh5
あっしの手には負えないので、
知恵袋からの引用と少し付けたし
00年東大文系
f(x，y)=1-ax-by-axy
fをxの関数と見れば高々1次式(一次関数)．
よって，最小になりうるのはx=-1 or 1のとき．
fをyの関数と見れば，高々1次式(一次関数)．
よって，最小になりうるのはx=-1 or 1のとき．
よって，-1≦x≦1，-1≦y≦1 におけるf(x，y)の
最小値の候補は
f(-1,-1)，f(-1，1)，f(1，-1)，f(1，1)しかなく，
これらがすべて正であることが必要十分．
f(-1,-1)=b+1>0
f(-1，1)=1+2a-b>0
f(1，-1)=1+b>0
f(1，1)=1-2a-b>0
以上より，-1<b かつ b<-2a+1 かつ b<2a+1
リンク
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1452773619?fr=sc_scdd&__ysp=eHnlubPpnaLjga7poJjln58gLTHiiaZ4IDEtYXgtYnktYXh5
管理人 2023/02/10(Fri) 01:07 No.55
∫つくときの符号変化
「0＜a(n)＜e-1/n!を示せ（a(n)=1/n!×∫x^n×e^(1-x)dxとする）」という問題で、解説に
0≦x≦1において
0≦x^n≦1
0≦x^n×e^(1-x)≦e^(1-x)
等号が成り立つのはx=0,1のときであるから、（★）
0＜∫x^n×e^(1-x)dx【積分区間：0→1】＜∫e^(1-x)dx【積分区間：0→1】
とあるのですが、（★）からの説明の意味が理解できず、どうして∫がついた途端＜の＝が消えたのでしょうか🤔？ここのところは前から謎だったので詳しく教えていただきたいです🙇♂
0≦x≦1において
0≦x^n≦1
0≦x^n×e^(1-x)≦e^(1-x)
等号が成り立つのはx=0,1のときであるから、（★）
0＜∫x^n×e^(1-x)dx【積分区間：0→1】＜∫e^(1-x)dx【積分区間：0→1】
とあるのですが、（★）からの説明の意味が理解できず、どうして∫がついた途端＜の＝が消えたのでしょうか🤔？ここのところは前から謎だったので詳しく教えていただきたいです🙇♂
Re: ∫つくときの符号変化
管理人 2023/01/27(Fri) 01:02 No.53
こんばんは。
分りやすくするために
f(x)=x^n×e^(1-x)
g(x)=e^(1-x)
とすると
0≦x≦1において
0≦f(x)≦g(x)
が成り立つということは、
g(x)の一部分がf(x)より大きいところがあるということですね。
このことは積分する(面積で考える)と、グラフが少しでも上にある方が面積が大きくなりませんか？
ですから等号が消えて常に∫g(x)dxが大きくなるのです。
f(x)≦g(x)は点で考えてますから等しいときもあれば、g(x)が大きいときもあるということで、積分(面積に)すると∫f(x)dxより∫g(x)dxが大きくなるということです。
以下のブログ記事の最後も参照ください。
https://mathtext.info/blog/2022/05/29/su3teisekifuto/
分りやすくするために
f(x)=x^n×e^(1-x)
g(x)=e^(1-x)
とすると
0≦x≦1において
0≦f(x)≦g(x)
が成り立つということは、
g(x)の一部分がf(x)より大きいところがあるということですね。
このことは積分する(面積で考える)と、グラフが少しでも上にある方が面積が大きくなりませんか？
ですから等号が消えて常に∫g(x)dxが大きくなるのです。
f(x)≦g(x)は点で考えてますから等しいときもあれば、g(x)が大きいときもあるということで、積分(面積に)すると∫f(x)dxより∫g(x)dxが大きくなるということです。
以下のブログ記事の最後も参照ください。
https://mathtext.info/blog/2022/05/29/su3teisekifuto/
管理人 2023/01/27(Fri) 01:02 No.53
∫つくときの符号変化
この問題の（2）の解説には
0≦x≦1において
0≦x^n≦1
0≦x^n×e^(1-x)≦e^(1-x)
等号が成り立つのはx=0,1のときであるから、（★）
0＜∫x^n×e^(1-x)dx【積分区間：0→1】＜∫e^(1-x)dx【積分区間：0→1】
とあるのですが、（★）からの説明の意味が理解できず、どうして∫がついた途端＜の＝が消えたのでしょうか🤔？ここのところは前から謎だったので詳しく教えていただきたいです🙇♂
0≦x≦1において
0≦x^n≦1
0≦x^n×e^(1-x)≦e^(1-x)
等号が成り立つのはx=0,1のときであるから、（★）
0＜∫x^n×e^(1-x)dx【積分区間：0→1】＜∫e^(1-x)dx【積分区間：0→1】
とあるのですが、（★）からの説明の意味が理解できず、どうして∫がついた途端＜の＝が消えたのでしょうか🤔？ここのところは前から謎だったので詳しく教えていただきたいです🙇♂
少し珍しい問題
次の連立不等式が表す領域をDとする時、以下の問いに答えよ。
y+|x|≦4
－y+|x|≦4
点（x,y）が領域Dを動く時、y+2xがとりうる値の最大値と最小値を求めよ。また、点（x,y）が領域Dを動く時、y+3｜x｜がとりうる値の最大値と最小値を求めよ。
y+|x|≦4
－y+|x|≦4
点（x,y）が領域Dを動く時、y+2xがとりうる値の最大値と最小値を求めよ。また、点（x,y）が領域Dを動く時、y+3｜x｜がとりうる値の最大値と最小値を求めよ。
Re: 少し珍しい問題
管理人 2023/01/26(Thu) 09:18 No.50
高校数学ですか🤔。自信がありませんが、答え書いてみました。
あってますかね？
珍しい問題なので何か引っかかってたり、
根本的に間違ってたりするかもしれませんが、間違いがあったら教えてくださいね😃
あってますかね？
珍しい問題なので何か引っかかってたり、
根本的に間違ってたりするかもしれませんが、間違いがあったら教えてくださいね😃
管理人 2023/01/26(Thu) 09:18 No.50
計算式
AとBの値を求める計算式を年寄りにもわかるように教えてください。
A＋B＝0.2112 B＝0.176AのときAとBを求める計算式
A＋B＝0.2112 B＝0.176AのときAとBを求める計算式
Re: 計算式
管理人 2023/01/19(Thu) 13:31 No.48
B=0.176A・・・(P)の両辺にAを足して
A＋B＝0.176A+A
A＋B=1.176A・・・①
これと
A＋B＝0.2112・・・②
から
①、②の右辺が等しいので
1.176A=0.2112としてAを求めて
Aを(P)に代入してBを求めればいいのかな？
計算はやってみてください。
それでは。
A＋B＝0.176A+A
A＋B=1.176A・・・①
これと
A＋B＝0.2112・・・②
から
①、②の右辺が等しいので
1.176A=0.2112としてAを求めて
Aを(P)に代入してBを求めればいいのかな？
計算はやってみてください。
それでは。
管理人 2023/01/19(Thu) 13:31 No.48