こんにちは。今回は定点Pから楕円への2本の接線が直交するようなとき, 定点Pの軌跡を求めてみようと思います。以下の問題が出題されるときは![]() の値が数値化されていることが多いです。今回は一般化ということで,
の値が数値化されていることが多いです。今回は一般化ということで, ![]() はそのままでやってみます。最後の関連記事も参考に。
はそのままでやってみます。最後の関連記事も参考に。
楕円の方程式![]() 定点P
定点P![]() とする。
とする。![]() のとき, 接線の1つは,
のとき, 接線の1つは, ![]() であり, このとき, 点Pは
であり, このとき, 点Pは![]() , または
, または![]() である。同様に,
である。同様に, ![]() のとき, 点Pは
のとき, 点Pは![]() ,
, ![]() である。したがって,
である。したがって, ![]() とすると,
とすると,
点Pを通る接線の方程式は![]() と表される。
と表される。
これを![]() に代入すると,
に代入すると, ![]()
両辺![]() かけて展開すると,
かけて展開すると, ![]()
![]()
これが重解を持てばいいので, 判別式![]() を用いると,
を用いると, ![]()
展開して, 接線の傾き![]() について整理すると
について整理すると![]()
![]() なので,
なので, ![]() で割って,
で割って, ![]()
となる。2本の接線の傾きを![]() とすると, 直交条件より,
とすると, 直交条件より, ![]() で,
で, ![]() はこの方程式の2つの解である。したがって, 解と係数の関係より,
はこの方程式の2つの解である。したがって, 解と係数の関係より, ![]()
が成り立つので, ![]()
![]()
よって, ![]() となり,
となり,
これは, ![]() を満たす。
を満たす。
したがって, 点Pが描く軌跡は, 中心が原点で半径![]() の円である。
の円である。
2接線が直交するとき
点Pから楕円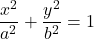 への2本の接線が直交するとき,
への2本の接線が直交するとき,
点Pが描く軌跡は, 中心が原点で半径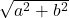 の円である。
の円である。
点Pが描く軌跡は, 中心が原点で半径
 高校数学:点(b, a)からの楕円の2接線は直交する
高校数学:点(b, a)からの楕円の2接線は直交する  高校数学:2次曲線:楕円の接線が直交するとき(横浜国立大)
高校数学:2次曲線:楕円の接線が直交するとき(横浜国立大) 数樂管理人のブログ
数樂管理人のブログ 

