無題
ここの掲示板は閉鎖しますね。
Re: 無題
 管理人
管理人  2023/10/14(Sat) 09:04 No.131
2023/10/14(Sat) 09:04 No.131
長らくご利用ありがとうございました。
 管理人
管理人  2023/10/14(Sat) 09:04 No.131
2023/10/14(Sat) 09:04 No.131
これはどうですか
X^(k+1)+Y^(k+1)≠-XY^(k)-X^(k)y+(x+y)z^(k)
X≧3 Y≧3 Z≧3とする
X≧3 Y≧3 Z≧3とする
Re: これはどうですか
 t原
t原  2023/10/13(Fri) 19:24 No.129
2023/10/13(Fri) 19:24 No.129
最後の方x、yが小文字ですが大文字と考えてくださいね
 t原
t原  2023/10/13(Fri) 19:24 No.129
2023/10/13(Fri) 19:24 No.129
方程式の文章題の質問
中学の数学の中間考査でわからない問題があったので質問させてください。問題 xについてax -2=bx +3で解は自然数、a、bは3以下の自然数である。この時考えられるa、bの値の組
は何組ありますか?
という問題です。よろしくお願いします。
は何組ありますか?
という問題です。よろしくお願いします。
Re: 方程式の文章題の質問
 管理人
管理人  2023/10/02(Mon) 05:59 No.127
2023/10/02(Mon) 05:59 No.127
方程式をそのまま解くと、
(a-b)x=5
x=5/(a-b)
となり、これが自然数ということは
a-b=1またはa-b=5
ここでa, bは3以下の自然数であることから
a-b=5となるa, bは存在しない。
a-b=1となる場合を考えると
a=3のときb=2
a=2のときb=1
の場合条件を満たす。
よって2組だと思います。
それでは。
(a-b)x=5
x=5/(a-b)
となり、これが自然数ということは
a-b=1またはa-b=5
ここでa, bは3以下の自然数であることから
a-b=5となるa, bは存在しない。
a-b=1となる場合を考えると
a=3のときb=2
a=2のときb=1
の場合条件を満たす。
よって2組だと思います。
それでは。
 管理人
管理人  2023/10/02(Mon) 05:59 No.127
2023/10/02(Mon) 05:59 No.127
No subject
またわからない問題が出てきてしまいました。
お手数をおかけしますが、説明していただけるとありがたいです。
よろしければ、お願い致します。
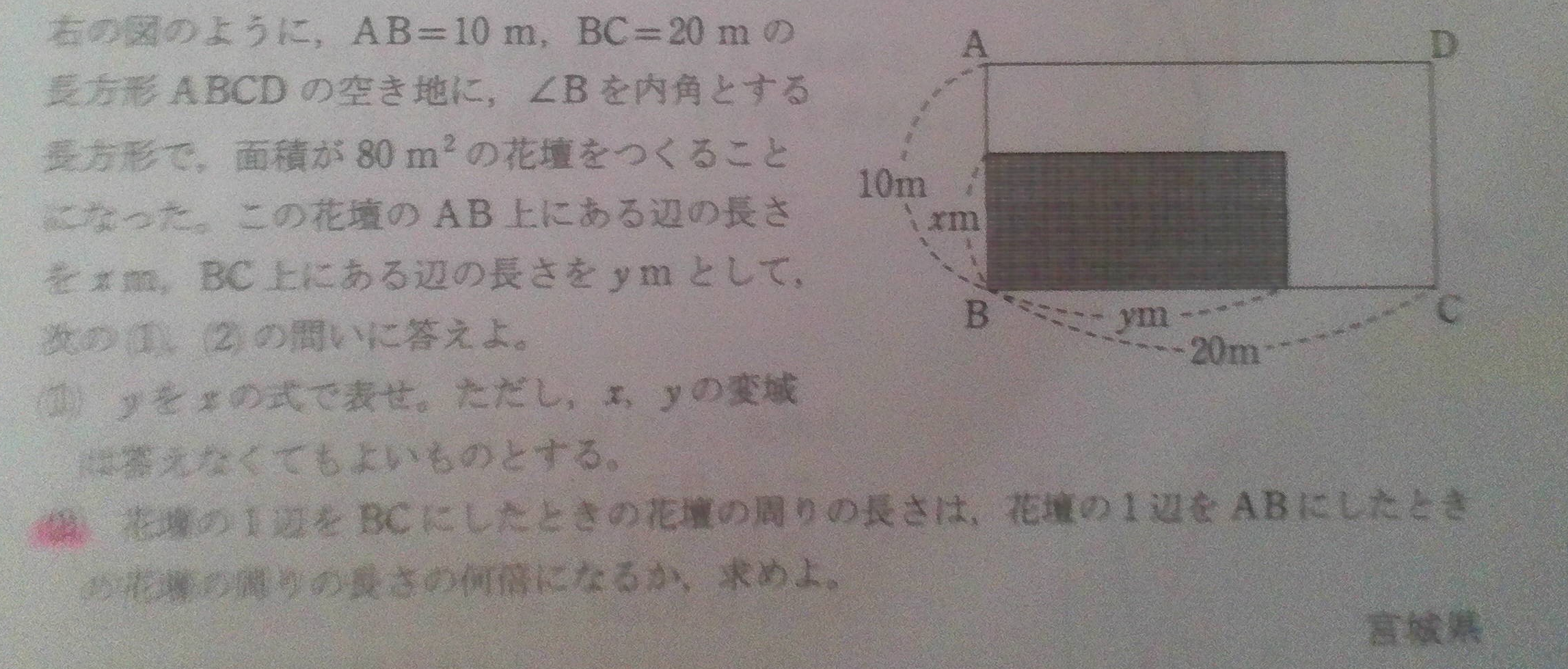
(1)の方はy=80/xと求められましたので、説明いただかなくて大丈夫です。
(2)の方が解けません。解説が載っていなくて、解き方がわかりませんでした。答えは、4/3倍です。
あと、問題文が読みづらいので、こちらにも書いておきます。
(2)花壇の一辺をBCにしたときの花壇の周りの長さは、花壇の1辺をABにしたときの花壇の周りの長さの何倍になるか求めよ。
長々としていて申し訳ありませんが、よろしくお願いします。
お手数をおかけしますが、説明していただけるとありがたいです。
よろしければ、お願い致します。
(1)の方はy=80/xと求められましたので、説明いただかなくて大丈夫です。
(2)の方が解けません。解説が載っていなくて、解き方がわかりませんでした。答えは、4/3倍です。
あと、問題文が読みづらいので、こちらにも書いておきます。
(2)花壇の一辺をBCにしたときの花壇の周りの長さは、花壇の1辺をABにしたときの花壇の周りの長さの何倍になるか求めよ。
長々としていて申し訳ありませんが、よろしくお願いします。
Re: No subject
 管理人
管理人  2023/10/01(Sun) 22:59 No.124
2023/10/01(Sun) 22:59 No.124
一辺がBCのとき縦は4
このとき周りの長さは24×2=48
一辺がABのとき横は8
このとき周りの長さは18×2=36
よって
48÷36=4/3
4/3倍
ですかね。
このとき周りの長さは24×2=48
一辺がABのとき横は8
このとき周りの長さは18×2=36
よって
48÷36=4/3
4/3倍
ですかね。
 管理人
管理人  2023/10/01(Sun) 22:59 No.124
2023/10/01(Sun) 22:59 No.124
Re: No subject
 流星__❼❷❽
流星__❼❷❽  2023/10/02(Mon) 05:25 No.126
2023/10/02(Mon) 05:25 No.126
解決しました!
説明していただき、ありがとうございました!🙇
説明していただき、ありがとうございました!🙇
 流星__❼❷❽
流星__❼❷❽  2023/10/02(Mon) 05:25 No.126
2023/10/02(Mon) 05:25 No.126
n¹⁰⁰(nの100乗)
正の整数nに対して、次のそれぞれの数の一の位の数が取りうる値をすべて求めなさい、という問題です。
n¹⁰⁰(nの100乗)は、どのように求めればよいのでしょうか?
説明していただけるとありがたいです。
よろしくお願いします。
n¹⁰⁰(nの100乗)は、どのように求めればよいのでしょうか?
説明していただけるとありがたいです。
よろしくお願いします。
Re:
 通行人
通行人  2023/09/26(Tue) 07:28 No.117
2023/09/26(Tue) 07:28 No.117
1,5,6?
 通行人
通行人  2023/09/26(Tue) 07:28 No.117
2023/09/26(Tue) 07:28 No.117
Re: n¹⁰⁰
 流星__❼❷❽
流星__❼❷❽  2023/09/26(Tue) 20:41 No.118
2023/09/26(Tue) 20:41 No.118
>>通行人様
答えてくださって、ありがとうございます。
それは、どうやって求めましたか?なにか法則とかがあるのでしょうか?
答えてくださって、ありがとうございます。
それは、どうやって求めましたか?なにか法則とかがあるのでしょうか?
 流星__❼❷❽
流星__❼❷❽  2023/09/26(Tue) 20:41 No.118
2023/09/26(Tue) 20:41 No.118
Re:
 通行人
通行人  2023/09/27(Wed) 08:00 No.119
2023/09/27(Wed) 08:00 No.119
0忘れてました。
0,1,5,6ですか?
10は何回かけても1の位は0
1は何回かけても1の位は1
2はかけると, 2, 4, 8, 6, 2・・・と1の位は2, 4, 8, 6の繰り返し, 4つのカタマリで動くので100÷4=25で割り切れるので100番目は6ってな感じで1~10調べるといいんじゃない?
0,1,5,6ですか?
10は何回かけても1の位は0
1は何回かけても1の位は1
2はかけると, 2, 4, 8, 6, 2・・・と1の位は2, 4, 8, 6の繰り返し, 4つのカタマリで動くので100÷4=25で割り切れるので100番目は6ってな感じで1~10調べるといいんじゃない?
 通行人
通行人  2023/09/27(Wed) 08:00 No.119
2023/09/27(Wed) 08:00 No.119
Re: n¹⁰⁰
 流星__❼❷❽
流星__❼❷❽  2023/09/29(Fri) 05:31 No.121
2023/09/29(Fri) 05:31 No.121
今、答えを見たら0,1,5,6となっていました
なるほど。ぜんぶ確かめないで、1〜10まで調べれば、答えが出るんですね!
ありがとうございます!
とても参考になりました!🙇
なるほど。ぜんぶ確かめないで、1〜10まで調べれば、答えが出るんですね!
ありがとうございます!
とても参考になりました!🙇
 流星__❼❷❽
流星__❼❷❽  2023/09/29(Fri) 05:31 No.121
2023/09/29(Fri) 05:31 No.121
 管理人
管理人